Graphmatica

Oleh : Halimah

Penggunaan Software Graphmatica

Graphmatica merupakan perangkat lunak pembuat grafik yang dibuat oleh kSoft, Inc. Graphmatica ini dapat digunakan mulai dari murid SMP yang baru mengenal grafik sampai dengan peneliti yang membutuhkan perangkat lunak penggambaran grafik sederhana.

Software Graphmatica ini mempunyai kelebihan dan kekurangan. Kelebihan dari software ini adalah mengetahui letak posisi (gambar) dari suatu persamaan ataupun pertidaksamaan linear, fungsi kuadrat dll dan ukurannya relatif kecil (di bawah satu megabyte) dan mudah digunakan. Sedangkan kekurangan yang terdapat pada sofware ini adalah untuk mengulang kesalahan "undo"  tidak bisa dilakukan sehingga, harus benar-benar teliti dalam pengerjaan soal menggunkan software ini. Dan kekurangan yang lain adalah tidak bisa menggambar grafik fungsi trigonometri. Materi yang akan saya bahas kali ini yaitu mengenai sistem persamaan dan pertidaksamaan  linier dua variabel dan persamaan garis singgung parabola.

Berikut adalah tampilan awal dari Graphmatica:

Untuk mengganti tampilan awal Graphmatica agar tidak bergridlines, yaitu dengan cara mengklik options-graph paper-none-ok.

Untuk background karena berwarna abu-abu dan terlihat gelap, maka kita ganti saja backgroundnya dengan cara mengklik options-graph paper-colors-pilih warna yang anda suka (saya merekomendasikan memilih warna putih agar terlihat jelas grafiknya nanti) kemudian klik ok.

Maka tampilan graphmatica yang baru seperti pada gambar si bawah ini :

Berikut adalah beberapa cara penggunaan Graphmatica:

1)      Tentukan himpunan penyelesaian dari sistem persamaan linier dua variabel berikut :

 2x+4y=10

 x-2y=5

 x≥0

 y≥0

Penyelesaian :

a.       Masukkan persamaan 2x + 4y = 10 di kotak yang panjang lalu tekan enter.

b.      Lalu masukkan pula persamaan x - 2y = 5 lalu tekan enter kembali.

c.       Setelah grafik tergambar, titik potong dari kedua grafik tersebut disebut himpunan penyelesaiannya. Untuk mengetahui titik potong dari kedua garis tersebut yaitu dengan klik tools, klik find intersection, lalu klik calculate. Maka himpunan penyelesaiannya yaitu (5,0). 

d.      Untuk memberi label himpunan penyelesaiannya yaitu dengan cara mengklik edit, pilih annotations, ketikkan HP pada kolom label, lalu klik place.

e.       Maka tampilan pada graphmaticanya seperti gambar di bawah ini :

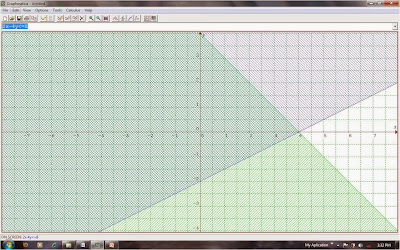
          2)      Tentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linier dua variabel berikut :

           2x - 4y ≤ 8

           2x + 2y ≤ 8

            x ≥ 0

            y ≥ 0

            Penyelesaian :

a.    Masukkan persamaan 2x - 4y ≤ 8 di kotak yang panjang , tetapi cara penulisan di kotaknya yaitu  2x - 4y <= 8, mengapa harus memakai tanda <= ? supaya persamaannya mudah dibaca oleh komputer, kalau anda memasukkan persamaannya dengan tanda≤ sudah pasti komputer tidak mau membaca/error. Setelah memasukkan persamaan pertama lalu  tekan enter.

b.      Lalu masukkan pula persamaan 2x + 2y ≤ 8 , penulisan di kotaknya menjadi 2x + 2y <= 8 lalu tekan enter kembali. 

c. Setelah grafik tergambar, titik potong dari kedua grafik tersebut disebut himpunan penyelesaiannya. Himpunan penyelesaiannya yaitu (4,0). Dan daerah himpunan penyelesaiaannya yaitu bagian yang terasir atau dilewati oleh dua grafik.

d.      Untuk memberi label himpunan penyelesaian dan daerah himpunan penyelsaiaannya yaitu dengan cara mengklik edit, pilih annotations, ketikkan HP pada kolom label untuk himpunan penyelesaian dan daerah himpunan penyelesaian untuk daerah himpunan penyelesaiannya, lalu klik place.

e.       Maka tampilan pada graphmaticanya seperti gambar di bawah ini :

3)      Tentukan garis singgung parabola dari persamaan x^2+2x-5y-9=0 dengan puncak (-1,-2) , di titik (4,3)!

Penyelesaian :

a.       Masukkan persamaan x^2+2x-5y-9=0 ke kotak yang paling panjang lalu tekan enter.

b.  Setelah itu, klik calculus – draw tangent. Kemudian klik sembarang titik pada parabola (misalkan, pada puncak parabolanya yaitu (-1,-2) Lalu akan muncul kotak draw tangent line.

c.     Di kotak draw tangen line terlihat bahwa persamaannya (equation) sudah benar yaitu x^2+2x-5y-9=0. Lalu masukkan x-nya 4 dan y-nya 3, karena garis singgung parabola tersebut pada titik (4,3). Kemudian klik calculate.

d.   Maka terbentuklah gambar persamaan garis singgungnya dengan persamaan garis singgung parabolanya (tangent line) y=2x-5 dengan kemiringan (slope/m) yaitu 2. 

e.  Untuk memberi label titik singggung persamaan garis singgung parabolanya, klik edit, pilih annotations, ketikkan TS pada kolom label, lalu klik place.

f.       Maka tampilan pada graphmatica nya seperti gambar di bawah ini :